Read But How Do It Know? - the Basic Principles of Computers for Everyone Online
Authors: J Clark Scott
But How Do It Know? - the Basic Principles of Computers for Everyone (10 page)

Do you remember Roman numerals? It is a number system that also consists of two elements. The first element is the symbols, just selected letters from the alphabet, ‘I’ for one, ‘V’ for five, ‘X’ for ten, ‘L’ for fifty, ‘C’ for one hundred, ‘D’ for five hundred, ‘M’ for one thousand. The second element is a method that allows you to represent numbers that don’t have a single symbol. The Roman method says that you write down multiple symbols, the largest ones first, and add them up, except when a smaller symbol is to left of a larger one, then you subtract it. So ‘II’ is two (add one and one,) and ‘IV’ is four (subtract one from five.) One of the things that made this author very happy about the coming of the year 2000 was the fact that Roman numerals representing the year got a lot simpler. 1999 was ‘MCMXCIX,’ you have to do three subtractions in your head just to read that one. 2000 was simply ‘MM.’
The normal number system we use today also consists of two ideas, but these are two very different ideas that came to us through Arabia rather than Rome. The first of these ideas is also about symbols, in this case 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. These digits are symbols that represent a quantity. The second idea is a method that we are so used to, that we use it instinctively. This method says that if you write down one digit, it means what it says. If you write down two digits next to each other, the one on the right means what it says, but the one to its left means ten times what it says. If you write down three digits right next to each other, the one on the right means what it says, the middle one means ten times what it says and the one on the left means one hundred times what it says. When you want to express a number greater than 9, you do it by using multiple digits, and you use this method that says that the number of positions to the left of the first digit tells you how many times you multiply it by ten before you add them up. So, if you have ‘246’ apples, that means that you have two hundred apples plus forty apples plus six apples.
So how does this work? A number of any amount can be written with the digits zero through nine, but when you go higher than nine, you have to use two digits. When you go above ninety-nine, you have to use three digits. Above nine hundred ninety-nine, you go to four digits, etc. If you are counting upwards, the numbers in any one of the positions go ‘round and ‘round - zero to nine, then zero to nine again, on and on, and whenever you go from nine back to zero, you increase the digit to the left by 1. So you only have ten symbols, but you can use more than one of them as needed and their positions with regard to each other specify their full value.
There is something odd about this in that the system is based on ten, but there is no single symbol for ten. On the other hand, there is something right about this – the symbols ‘0’ through ‘9’ do make up ten different symbols. If we also had a single symbol for ten, there would actually be eleven different symbols. So whoever thought of this was pretty smart.
One of the new ideas in this Arabic system was to have a symbol for zero. This is useful if you want to say that you have zero apples, but it is also a necessary thing to keep the positions of the digits straight. If you have 50 apples or 107 apples, you need the zeros in the numbers to know what position each digit is actually in, so you can multiply by ten the correct number of times.
Now these two ideas in the Arabic number system (the digits and the method) have one thing in common. They both have the number ten associated with them. There are ten different digits, and as you add digits to the left side of a number, each position is worth ten times more than the previous one.
In school, when they first teach children about numbers, they say something about our number system being based on the number ten, because we have ten fingers. So here’s an odd question: What if this number system had been invented by three-toed sloths? They only have three fingers on each hand, and no thumbs. They would have invented a number system with only six digits- 0, 1, 2, 3, 4 and 5. Could this work? If you had eight apples, how would you write it? There is no number ‘8’ in this system. The answer is, that since the first idea, the digits, was changed to only have six digits, then the second idea, the method, would also have to be changed so that as you add positions to the left, each one would have to be multiplied by sixes instead of tens. Then this system would work. As you count your apples, you would say “0, 1, 2, 3, 4, 5…” and then what? There’s no ‘6’ for the next number. Well, according to the method, when you want to go beyond the highest digit, you go back to ‘0’ and add a ‘1’ to the left. OK, “0, 1, 2, 3, 4, 5, 10, 11, 12.” Now you have counted all of your apples. What would this ‘12’ mean? It would be this many: . I guess you’d call it eight, but you’d write it ‘12’. Very odd, but it does work out - 1 times six plus two equals eight apples, it follows the Arabic method, but it is based on six instead of ten. If you continued counting up, when you got to ‘15,’ which is
. I guess you’d call it eight, but you’d write it ‘12’. Very odd, but it does work out - 1 times six plus two equals eight apples, it follows the Arabic method, but it is based on six instead of ten. If you continued counting up, when you got to ‘15,’ which is (one times six plus five,) the next number would be ‘20,’ but the ‘2’ would mean two sixes, or this many:
(one times six plus five,) the next number would be ‘20,’ but the ‘2’ would mean two sixes, or this many: . And 55 would be followed by 100. The ‘1’ in that third position would be how many ‘36’s there were (six times six)
. And 55 would be followed by 100. The ‘1’ in that third position would be how many ‘36’s there were (six times six)
This is a very odd number system, but guess what, you already use it in your everyday life. Yes, think of the way we write time, or the kind of clock that shows the numbers on its face. The right digit of the minutes and seconds follows our normal numbers, 0-9, 0-9, over and over. But the left digit of the minutes and seconds only goes 0-5. After 59 minutes, the clock goes to the next hour and 00 minutes. There are 60 minutes in an hour, numbered from 00 to 59. That left position never gets over 5. That position uses the number system based on six symbols (0-5). The hour part of the clock tells how many ‘60’s there are, though you will never see a 60 on the face of the clock. And you are so used to this that you don’t have to think about it. When the clock says 1:30, you know that this is halfway between 1:00 and 2:00, you don’t have to do any math in your head to figure it out. Have you ever had to add time? If you add 40 minutes and 40 minutes, you get 80 minutes, but to write that down in hours and minutes, you have to figure out how many 60s there are in 80, in this case 1, then figure out how many minutes there are beyond 60, in this case 20. So you write 1:20. The 1 represents 60 minutes, add 20 and you have your 80 again. So this is pretty complicated, two different number systems in the same number! But you have already been using it your whole life.

The hour positions are even stranger. On a 12 hour clock, it skips zero and goes 1-12 AM, then 1-12 PM. On a 24 hour clock, it goes from 00-23. We won’t try to analyze these. The point we wanted to make was that you are already familiar with number systems based on numbers other than ten.
You could invent a number system for any amount of digits, 10 or 6 like we’ve seen above, or 3 or 14 or any number you choose. But the simplest one would be if you only had 2 digits, 0 and 1. How would this one work? Well, you’d count 0, 1… and then you’re already out of digits – so back to 0 and add 1 on the left, making the next number 10 then 11, then you’re out of digits again, so 100 then 101, 110, 111 then 1000. This system is based on two, so there are only two digits, and as you add positions to the left, each one is worth two times more than the previous one. The right position means what it says, the next one to the left means two times what it says, the next means four times what it says, the next means eight times, etc. When you get down to only having two possible digits, you don’t have to do much multiplication to figure out the total value of a position. In the position that is worth ‘eight,’ for example, there can only be a one, meaning one ‘eight,’ or a zero, meaning ‘no eights.’
While we’re at it, let’s imagine a very strange animal with eight fingers on each hand. That animal would have invented numbers based on sixteen. In their system, they would be able to write ten through fifteen each with a single symbol. Only when they arrived at sixteen would they get back around to 0 and need to put a 1 in the position to the left. To see how this would work, we need six new symbols, so let’s just use the first six letters of the alphabet. ‘A’ will mean ten, ‘B’ will mean eleven, ‘C’ will mean twelve, ‘D’ will mean thirteen, ‘E’ will mean fourteen and ‘F’ will mean fifteen. Only after using all sixteen symbols in the right position will we run out of symbols, and the next number will be sixteen, written ‘10’ in this system. If you’re familiar with the pounds and ounces system of weights, it’s sort of like this system. There are 16 ounces in a pound, so you know that 8 ounces is half a pound. Adding 9 ounces and 9 ounces comes out to 1 pound 2 ounces.
Here is a chart that shows five different number systems. The first column is the old tally mark system to keep it sensible.
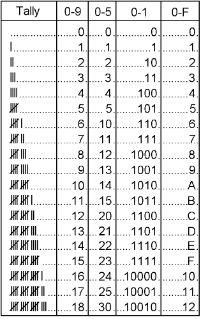
Our normal 0-9 numbers are called the decimal system, because ‘dec’ means ten in some ancient language. The 0-5 system would be called the senary system, because ‘sen’ means six in some other ancient language. This new system with just 0 and 1 is called the binary system because ‘bi’ means two, also because of some ancient language. This other new system, the 0-F system, will be called the hexadecimal system, because ‘hex’ is another ancient word that means six and ‘dec’ still means ten, so it’s the six plus ten system.
